[DirectX11] Specular BRDF

 

Diffuse의 경우에는 간단하게 램버트의 코사인 법칙을 적용했다.

다음으로 Specular를 계산해야하는데 Phong 반사 모델 같은 간단한 방법도 있지만 그것보다는 더 자연스럽게 표현하고싶어서 Cook-Torrance 방식을 적용했다.

 

코드와 수식 참고한곳:

https://blog.naver.com/canny708/221551990444

GGX와 Schlick Fresnel, 그리고 자주 쓰이는 쿡-토런스 함수

https://graphicrants.blogspot.com/2013/08/specular-brdf-reference.html?m=0

Specular BRDF Reference

 

 

---

 

 

 

Cook-Torrance의 specular 계산식은 아래와 같다.

 

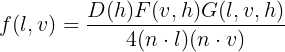
D는 Normal Distribution Function으로 NDF라고 줄여서 쓴다.

F는 Fresnel

G는 Geometric Shadowing이다.

 

l은 빛 벡터

v는 카메라 벡터

n은 물체의 노멀 벡터

h는 Half 벡터다.

Half 벡터는 빛 벡터와 카메라 벡터를 더하고 정규화한 벡터다.

 

---

 

NDF

D 함수는 GGX를 사용했다.

float D_GGX(float a2, float NdotH)
{
    float d = (NdotH * a2 - NdotH) * NdotH + 1;
    return a2 / (PI * d * d);
}

여기에서 a는 Roughness의 제곱이고, a2는 a의 제곱이다.

 

 

왼쪽부터 Roughness 0.8 -> 0.6 -> 0.4 -> 0.2

 

---

 

Fresnel

Fresnel 함수는 Cook-Torrance의 함수와 Schlick의 함수가 있다.

 

 

 

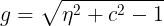
F0은 반사율(reflectance)이다.

float3 F_Schlick(float3 SpecularColor, float VdotH)
{
    float Fc = pow(1 - VdotH, 5);
    return saturate(50.f * SpecularColor.g) * Fc + (1 - Fc) * SpecularColor;
}

float3 F_Schlick_2(float3 F0, float VdotH)
{
    return F0 + (1 - F0) * pow(1 - VdotH, 5);
}

// F0 == Reflectance
float3 F_Schlick_3(float F0, float VdotH)
{
    return F0 + (1 - F0) * pow(1 - VdotH, 5);
}

float3 F_CookTorrance(float3 SpecularColor, float VdotH)
{
    float3 SpecularColorSqrt = sqrt(clamp(SpecularColor, float3(0.f, 0.f, 0.f), float3(0.99f, 0.99f, 0.99f)));
    float3 n = (1 + SpecularColorSqrt) / (1 - SpecularColorSqrt);
    float3 g = sqrt(n * n + VdotH * VdotH - 1);
    return 0.5f * pow((g - VdotH) / (g + VdotH), 2) * (1 + pow(((g + VdotH) * VdotH - 1) / ((g - VdotH) * VdotH + 1), 2));
}

Specular에 색상을 입력받는 함수도 있고, F0값을 받는 함수도 있다.

Cook-Torrance보다는 Schlick이 더 가볍다.

 

왼쪽: Schlick, 오른쪽: Cook-Torrance

Specular 색을 빨간색으로 한 결과다.

빛을 받는 면을 비교하면 두 식의 차이는 거의 없다.

 

왼쪽: Schlick, 오른쪽: Cook-Torrance

하지만 빛이 물체 뒤에 있는 경우에는 색을 다루는 방식의 차이 때문에 색상 차이가 있다.

최종 결과에서는 특정 각도에서 작은 부분에서만 차이가 나기 때문에 어느 것을 사용해도 문제되진 않을 듯 하다.

 

아래는 그래프로 비교한 결과다.

 

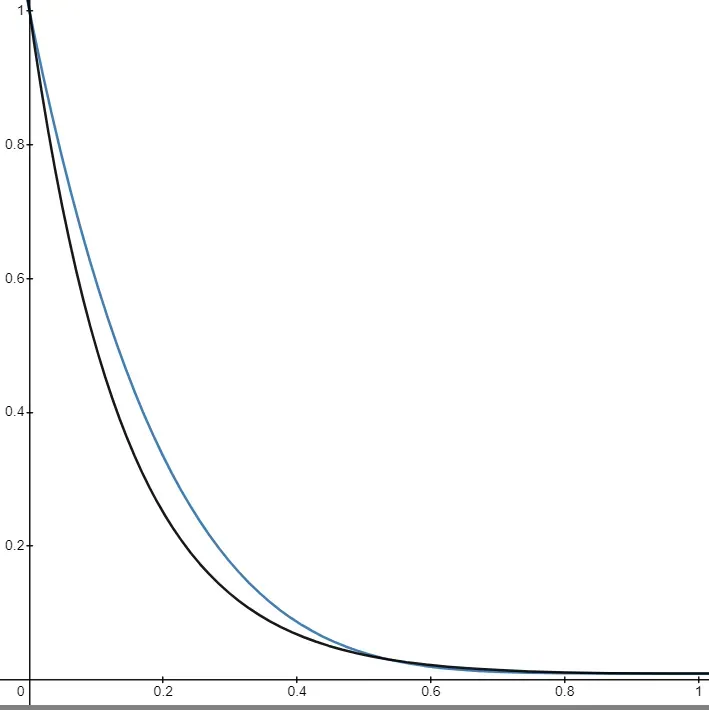
파란색: Schlick, 검은색: Cook-Torrance

x축은 카메라 벡터와 Half벡터의 내적값

y축은 Fresnel 결과값

F0은 0에서부터 1으로 점점 늘어나게 했다.

https://www.desmos.com/calculator/v1vdlrvs1o

Desmos | 그래핑 계산기

 

 

---

 

Geometric Shadowing

G 함수에는 여러가지가 있지만 그 중에서 Smith의 방식으로는 G 함수가 두개의 요소로 나눠진다.

 

 

그리고 Smith의 G함수는 다음과 같다.

 

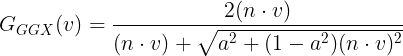
v를 대입해서 한번 계산하고 l을 대입해서 한번 더 계산한 다음 서로 곱해야 한다.

근사값을 계산하는 Schlick-Beckmann 함수도 있다.

 

 

Schlick-Beckmann의 G 함수

 

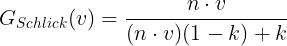
그런데 이 함수는 Smith의 잘못된 버전이라는 주장이 있어서 사용하기 전에 Smith의 방식과 비교해보라고 한다.

 

그래프로 비교해보면 이렇다.

 

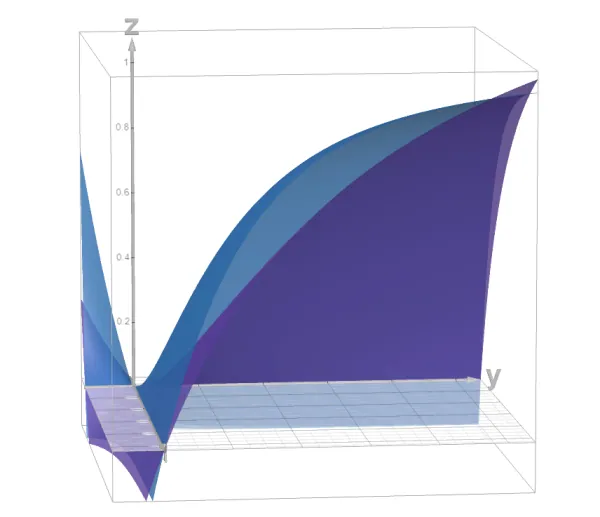
파란색: Smith, 보라색: Schlick-Beckmann

https://www.desmos.com/3d/a404adad7b

Desmos | 3D 그래핑 계산기

 

float G_Smith(float a2, float NdotV, float NdotL)
{
    float G_SmithV = NdotV + sqrt(NdotV * (NdotV - NdotV * a2) + a2);
    float G_SmithL = NdotL + sqrt(NdotL * (NdotL - NdotL * a2) + a2);
    return (4 * NdotV * NdotL) / (G_SmithV * G_SmithL);
}

float G_SchlickBeckmann(float a, float NdotV, float NdotL)
{
    float k = a * sqrt(2 / PI);
    float G_SchlickV = NdotV * (1 - k) + k;
    float G_SchlickL = NdotL * (1 - k) + k;
    return (NdotV / G_SchlickV) * (NdotL / G_SchlickL);
}

 

위: Schlick-Beckmann, 아래: Smith, 왼쪽부터 Roughness 0.8 -> 0.6 -> 0.4 -> 0.2

Schlick-Beckmann의 경우 빛을 받지 못하는 쪽은 밝게되는데 이 부분은 최종 결과에 영향을 주지 않는다.

 

 

 

---

 

 

 

마지막으로 각 값을 곱하면 된다.

 

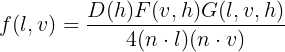
float3 HalfDir = normalize(LightDir + ViewDir);

float a = pow(Roughness, 2);
float a2 = pow(a, 2);
float NdotV = max(dot(Normal, ViewDir), 0);
float NdotL = max(dot(Normal, LightDir), 0);
float VdotH = max(dot(ViewDir, HalfDir), 0);
float NdotH = max(dot(Normal, HalfDir), 0);

float D = D_GGX(a2, NdotH);
float3 F = F_Schlick_2(SpecColor, VdotH);
float G = G_SchlickBeckmann(a, NdotV, NdotL);

float3 Rs = (D * F * G) * saturate(1 / (4 * NdotL * NdotV + 0.0001));

값과 식을 잘못 적용하면 문제가 생길 수 있다.

최대한 문제가 발생하지 않도록 내적 값과 식을 위와 같이 적용했다.

 

---

 

참고로 Geometric Shadowing의 Smith 식을 보면 분자에 4 * (n  ·  l) * (n · v)가 들어가는데 Specular 계산 식을 보면 동일한 값으로 나누게 되어있다.

이걸 이용해서 다음과 같이 식을 간소화 할 수도 있다고 한다.

float G_SmithOptimized(float a2, float NdotV, float NdotL)
{
    float G_SmithV = NdotV + sqrt(NdotV * (NdotV - NdotV * a2) + a2);
    float G_SmithL = NdotL + sqrt(NdotL * (NdotL - NdotL * a2) + a2);
    return 1.f / (G_SmithV * G_SmithL);
}



// ...
float3 Rs = D * F * G_SmithOptimized(a2, NdotV, NdotL);

개인적인 경험으로는 아래처럼 잘못된 결과가 나와서 사용하지 않기로 했다.

 

잘못 적용된 결과

 

---

 

최종 결과는 아래와 같다.

D: GGX

F: Schlick

G: Schlick-Beckmann

왼쪽부터 Roughness 0.8 -> 0.6 -> 0.4 -> 0.2